The ergmito’s workhorse are two other functions: (1) ergm’s ergm.allstats which is used to compute the support of model’s sufficient statistics, and (2) ergmito_formulae which is a wrapper of that same function, and that returns a list including the following two functions: loglike and grad, the functions to calculate the joint log-likelihood of the model and its gradient.

library(ergmito)
data(fivenets)
model_object <- ergmito_formulae(fivenets ~ edges + ttriad)

# Printing the model object
model_object
#> ergmito log-likelihood function
#> Number of networks:  5 
#> Model:  fivenets ~ edges + ttriad 
#> Available elements by using the $ operator:
#> loglik: function (params, ..., as_prob = FALSE, total = TRUE) grad  : function (params, ...)

# Printing the log-likelihood function
model_object$loglik
#> function (params, ..., as_prob = FALSE, total = TRUE) 
#> {
#>     if (total) {
#>         ans <- sum(exact_loglik(ergmito_ptr, params = params, 
#>             ..., as_prob = as_prob))
#>         if (!as_prob && !is.finite(ans)) 
#>             return(-.Machine$double.xmax * 1e-100)
#>         else return(ans)
#>     }
#>     else {
#>         exact_loglik(ergmito_ptr, params = params, ..., as_prob = as_prob)
#>     }
#> }
#> <bytecode: 0x72fe538>
#> <environment: 0x72f8d60>

Besides of the log-likelihood function and the gradient function, ergmito_formulae also returns We can take a look at each component from our previous object:

# The vectors of weights
str(model_object$stats_weights)
#> List of 5
#>  $ : num [1:40] 66 12 168 72 48 196 120 1 88 1 ...
#>  $ : num [1:40] 66 12 168 72 48 196 120 1 88 1 ...
#>  $ : num [1:40] 66 12 168 72 48 196 120 1 88 1 ...
#>  $ : num [1:40] 66 12 168 72 48 196 120 1 88 1 ...
#>  $ : num [1:40] 66 12 168 72 48 196 120 1 88 1 ...

# The matrices of the sufficient statistics
str(model_object$stats_statmat)
#> List of 5
#>  $ : num [1:40, 1:2] 2 1 4 8 7 3 6 12 6 0 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : chr [1:2] "edges" "ttriple"
#>  $ : num [1:40, 1:2] 2 1 4 8 7 3 6 12 6 0 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : chr [1:2] "edges" "ttriple"
#>  $ : num [1:40, 1:2] 2 1 4 8 7 3 6 12 6 0 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : chr [1:2] "edges" "ttriple"
#>  $ : num [1:40, 1:2] 2 1 4 8 7 3 6 12 6 0 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : chr [1:2] "edges" "ttriple"
#>  $ : num [1:40, 1:2] 2 1 4 8 7 3 6 12 6 0 ...
#>   ..- attr(*, "dimnames")=List of 2
#>   .. ..$ : NULL
#>   .. ..$ : chr [1:2] "edges" "ttriple"

# The target statistic
model_object$target_stats
#>      edges ttriple
#> [1,]     2       0
#> [2,]     7       4
#> [3,]     4       0
#> [4,]     5       2
#> [5,]     2       0

All this is closely related to the output object from the function ergm.allstats. The next section shows how all this works together to estimate the model parameters using Metropolis-Hastings MCMC.

Example: Bayesian inference with fivenets

Suppose that we have a prior regarding the distribution of the fivenets model: The edges parameter is normally distributed with mean -1 and variance 2, while the nodematch("female") term has the same distribution but with mean 1. We can implement this model using a Metropolis-Hastings ratio. First, we need to define the log of the posterior distribution:

# Analyzing the model
model_object <- ergmito_formulae(fivenets ~ edges + nodematch("female"))
#> Warning: `set_attrs()` is deprecated as of rlang 0.3.0
#> This warning is displayed once per session.

# Defining the logposterior
logposterior <- function(p) {
  model_object$loglik(params = p) +
  sum(dnorm(p, mean = c(-1,1), sd = sqrt(2), log = TRUE))
}

For this example, we are using the fmcmc R package. Here is how we put everything together:

# Loading the required R packages
library(fmcmc)
library(coda)

# Is it working?
logposterior(c(-1, 1))
#> [1] -38.24283

# Now, calling the MCMC function from the fmcmc R package
ans <- MCMC(
  fun     = logposterior,
  initial = c(0, 0),
  # 5,000 steps sampling one of every ten iterations
  nsteps  = 5000,
  thin    = 10,
  # We are using a normal transition kernel with .5 scale and updates are done
  # one variable at a time in a random order
  kernel = kernel_normal(scale = .5, scheme = "random")
  )

We can now visualize our results. Since the resulting object is of class mcmc.list, which is implemented in the coda R package for MCMC diagnostics, we can use all the methods included in the package:

plot(ans)

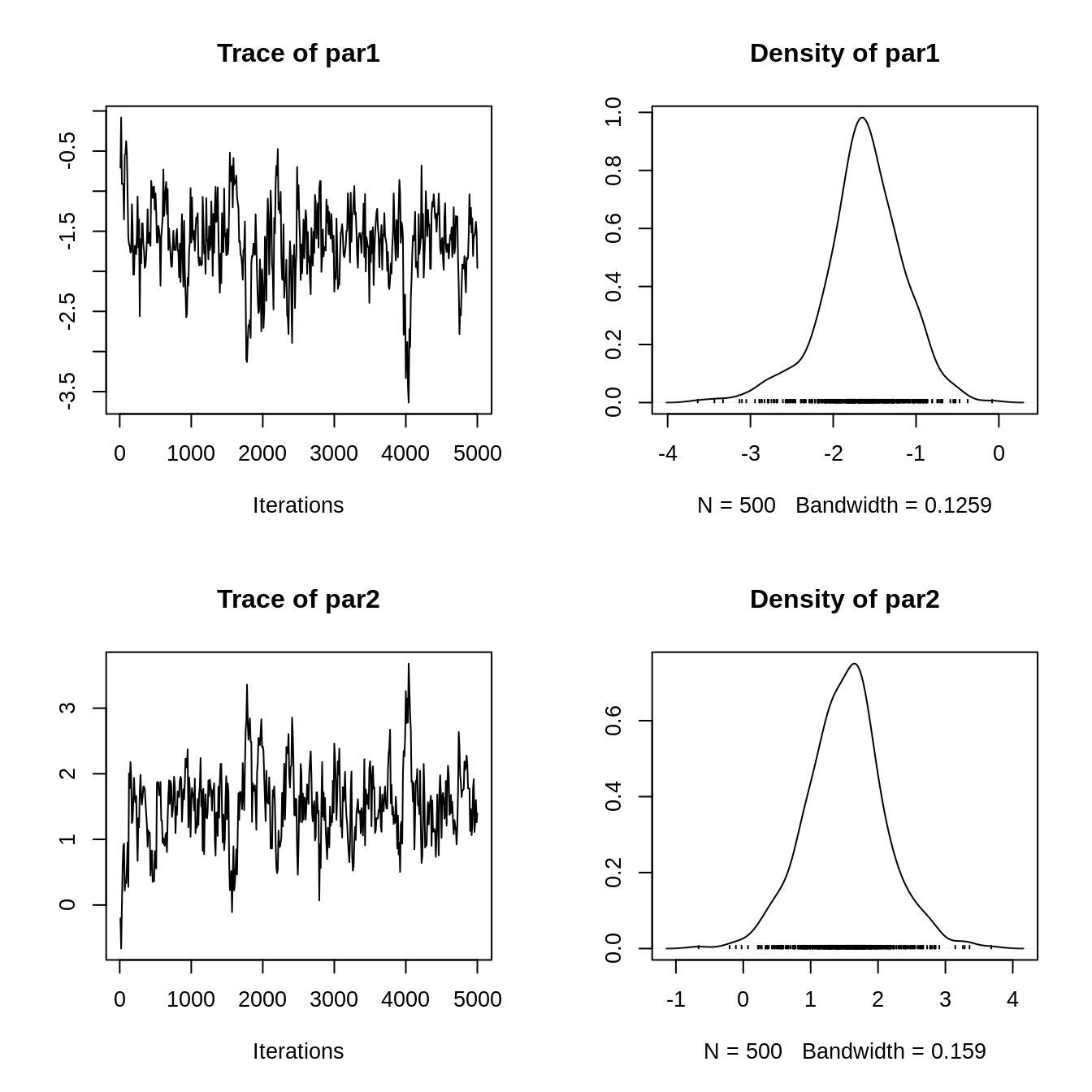
summary(ans)
#> 
#> Iterations = 10:5000
#> Thinning interval = 10 
#> Number of chains = 1 
#> Sample size per chain = 500 
#> 
#> 1. Empirical mean and standard deviation for each variable,
#>    plus standard error of the mean:
#> 
#>        Mean     SD Naive SE Time-series SE
#> par1 -1.636 0.4872  0.02179        0.05699
#> par2  1.517 0.5813  0.02600        0.06940
#> 
#> 2. Quantiles for each variable:
#> 
#>         2.5%    25%    50%    75%   97.5%
#> par1 -2.7822 -1.881 -1.624 -1.329 -0.7182
#> par2  0.3567  1.158  1.540  1.855  2.7509

Finally, we can compare this result with what we obtain from the ergmito function

summary(ergmito(fivenets ~ edges + nodematch("female")))
#> Warning: The observed statistics (target.statistics) are near or at the boundary
#> of its support, i.e. the Maximum Likelihood Estimates maynot exist or be hard to
#> be estimated. In particular, the statistic(s) "edges", "nodematch.female".
#> 
#> ERGMito estimates (MLE)
#> This model includes 5 networks.
#> 
#> formula:
#>   fivenets ~ edges + nodematch("female")
#> 
#>                  Estimate Std. Error z value Pr(>|z|)   
#> edges            -1.70475    0.54356 -3.1363 0.001711 **
#> nodematch.female  1.58697    0.64305  2.4679 0.013592 * 
#> ---
#> Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
#> AIC: 73.34109    BIC: 77.52978    (Smaller is better.)

Extending ergmito

George G. Vega Yon

2020-08-09

Example: Bayesian inference with fivenets