This R package, which has been developed on top of the amazing work that the Statnet team has done, implements estimation and simulation methods for Exponential Random Graph Models of small networks, in particular, up to 5 vertices for directed graphs and 7 for undirected networks. In the case of small networks, the calculation of the likelihood of ERGMs becomes computationally feasible, which allows us avoiding approximations and do exact calculation, ultimately obtaining MLEs directly.
Checkout the examples section, and specially the Using interaction effects example.
Support
This material is based upon work support by, or in part by, the U.S. Army Research Laboratory and the U.S. Army Research Office under grant number W911NF-15-1-0577
Computation for the work described in this paper was supported by the University of Southern California’s Center for High-Performance Computing (hpcc.usc.edu).
Citation
When using ergmito, always cite this paper
Vega Yon G, Slaughter A, de la Haye K (2020). “Exponential Random Graph models for Little Networks.” Social Networks. doi: 10.1016/j.socnet.2020.07.005 (URL: https://doi.org/10.1016/j.socnet.2020.07.005), in press.
Use this if you are using the GitHub version of ergmito:
Vega Yon G (2020). ergmito: Exponential Random Graph Models for Small Networks. R package version 0.3-0 (wip), <URL: https://github.com/muriteams/ergmito>.
Use this if you are using the CRAN version of ergmito:
Vega Yon G (2020). ergmito: Exponential Random Graph Models for Small Networks. R package version 0.3-0, <URL: https://cran.r-project.org/package=ergmito>.
To see these entries in BibTeX format, use ‘print(
Installation
The development version from GitHub with:
# install.packages("devtools") devtools::install_github("muriteams/ergmito")
This requires compilation. Windows users can download the latest compiled version from appveyor here. The file to download is the one named ergmito_[version number].zip. Once downloaded, you can install typing the following:
install.packages("[path to the zipfile]/ergmito_[version number].zip", repos = FALSE)
In the case of Mac users, and in particular, those with Mojave version, they may need to install the following https://github.com/fxcoudert/gfortran-for-macOS/releases
Examples
Quick run
In the following example we simulate a small network with 4 vertices and estimate the model parameters using ergm and ergmito. We start by generating the graph
# Generating a small graph library(ergmito) library(ergm) library(sna) set.seed(12123) n <- 4 net <- rbernoulli(n, p = .3) gplot(net)
To estimate the model
# ERGM (estimation via MC-MLE) ans_ergm <- ergm(model, control = control.ergm( MCMC.effectiveSize = 4000, seed = 444) ) # The ergmito should have a larger value ergm.exact(ans_ergmito$coef, model) > ergm.exact(ans_ergm$coef, model) #> [,1] #> [1,] TRUE summary(ans_ergmito) #> #> ERGMito estimates (MLE) #> This model includes 1 networks. #> #> formula: #> net ~ edges + istar(2) #> #> Estimate Std. Error z value Pr(>|z|) #> edges -1.37749 1.00260 -1.3739 0.1695 #> istar2 0.50653 1.32701 0.3817 0.7027 #> AIC: 17.36312 BIC: 18.33294 (Smaller is better.) summary(ans_ergm) #> #> ========================== #> Summary of model fit #> ========================== #> #> Formula: net ~ edges + istar(2) #> #> Iterations: 2 out of 20 #> #> Monte Carlo MLE Results: #> Estimate Std. Error MCMC % z value Pr(>|z|) #> edges -1.4110 0.9995 0 -1.412 0.158 #> istar2 0.5607 1.3719 0 0.409 0.683 #> #> Null Deviance: 16.64 on 12 degrees of freedom #> Residual Deviance: 13.35 on 10 degrees of freedom #> #> AIC: 17.35 BIC: 18.32 (Smaller is better.)
Estimating data with known parameters
The following example shows the estimation of a dataset that is included in the package, fivenets. This set of five networks was generated using the new_rergmito function which allows creating a function to draw random ERGMs with a fixed set of parameters, in this case, edges = -2.0 and nodematch("female") = 2.0
data(fivenets) model1 <- ergmito(fivenets ~ edges + nodematch("female")) summary(model1) # This data has know parameters equal to -2.0 and 2.0 #> #> ERGMito estimates (MLE) #> This model includes 5 networks. #> #> formula: #> fivenets ~ edges + nodematch("female") #> #> Estimate Std. Error z value Pr(>|z|) #> edges -1.70475 0.54356 -3.1363 0.001711 ** #> nodematch.female 1.58697 0.64305 2.4679 0.013592 * #> --- #> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 #> AIC: 73.34109 BIC: 77.52978 (Smaller is better.)
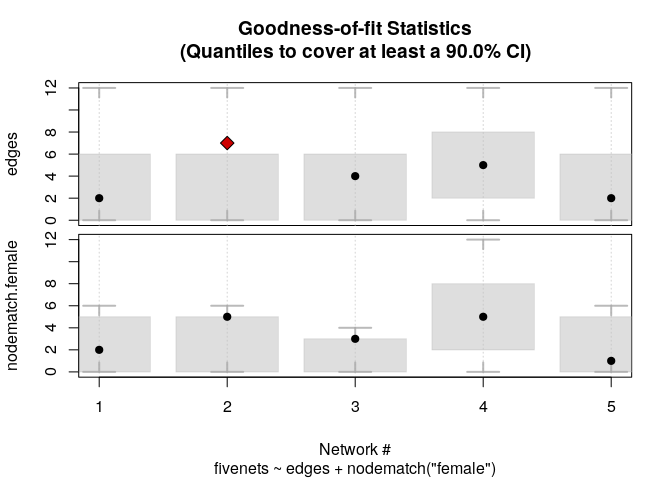
We can also compute GOF
fivenets_gof <- gof_ergmito(model1) fivenets_gof #> #> Goodness-of-fit for edges #> #> obs min mean max lower upper lower prob. upper prob. #> net 1 2 0 3.746607 12 0 6 0.008080856 0.9635261 #> net 2 7 0 3.746607 12 0 6 0.008080856 0.9635261 #> net 3 4 0 3.113122 12 0 6 0.020642814 0.9881036 #> net 4 5 0 5.647059 12 2 8 0.030934588 0.9514908 #> net 5 2 0 3.746607 12 0 6 0.008080856 0.9635261 #> #> #> Goodness-of-fit for nodematch.female #> #> obs min mean max lower upper lower prob. upper prob. #> net 1 2 0 2.823530 6 0 5 0.02201716 0.9891396 #> net 2 5 0 2.823530 6 0 5 0.02201716 0.9891396 #> net 3 3 0 1.882353 4 0 3 0.07855507 0.9509584 #> net 4 5 0 5.647059 12 2 8 0.03093459 0.9514908 #> net 5 1 0 2.823530 6 0 5 0.02201716 0.9891396 #> #> Note: Exact confidence intervals where used. This implies that the requestes CI may differ from the one used (see ?gof_ergmito). plot(fivenets_gof)
Fitting block-diagonal models
The pooled model can be also compared to a block-diagonal ERGM. The package includes three functions to help with this task: blockdiagonalize, splitnetwork, and ergm_blockdiag.
data("fivenets") # Stacking matrices together fivenets_blockdiag <- blockdiagonalize(fivenets, "block_id") fivenets_blockdiag # It creates the 'block_id' variable #> Network attributes: #> vertices = 20 #> directed = TRUE #> hyper = FALSE #> loops = FALSE #> multiple = FALSE #> bipartite = FALSE #> total edges= 20 #> missing edges= 0 #> non-missing edges= 20 #> #> Vertex attribute names: #> block_id female name_original vertex.names #> #> No edge attributes
# Fitting the model with ERGM ans0 <- ergm( fivenets_blockdiag ~ edges + nodematch("female"), constraints = ~ blockdiag("block_id") )
ans1 <- ergm_blockdiag(fivenets ~ edges + nodematch("female"))
# Now with ergmito ans2 <- ergmito(fivenets ~ edges + nodematch("female")) # All three are equivalent cbind( ergm = coef(ans0), ergm_blockdiag = coef(ans1), ergmito = coef(ans2) ) #> ergm ergm_blockdiag ergmito #> edges -1.704748 -1.704748 -1.704748 #> nodematch.female 1.586965 1.586965 1.586965
The benefit of ergmito:
t_ergm <- system.time(ergm( fivenets_blockdiag ~ edges + nodematch("female") + ttriad, constraints = ~ blockdiag("block_id") )) t_ergmito <- system.time( ergmito(fivenets ~ edges + nodematch("female") + ttriad) )
# Relative elapsed time (t_ergm/t_ergmito)[3] #> elapsed #> 110.6667
Fitting a large model
Suppose that we have a large sample of small networks (ego from Facebook, Twitter, etc.), 20,000 which account for 80,000 vertices:
set.seed(123) bignet <- rbernoulli(sample(3:5, 20000, replace = TRUE)) # Number of vertices sum(nvertex(bignet)) #> [1] 80089
We can fit this model in a memory efficient way.
system.time(ans0 <- ergmito(bignet ~ edges + mutual)) #> user system elapsed #> 2.971 0.021 2.991 summary(ans0) #> #> ERGMito estimates #> #> formula: bignet ~ edges + mutual #> #> Estimate Std. Error z value Pr(>|z|) #> edges -0.0020193 0.0068675 -0.2940 0.7687 #> mutual -0.0018160 0.0112247 -0.1618 0.8715 #> AIC: 352097.2 BIC: 352118.1 (Smaller is better.)
Using interaction effects
One advantage of using exact statistics is the fact that we have significantly more flexibility when it comes to specifying sufficient statistics. Just like one would do when working with Generalized Linear Models in R (the “glm” function), users can alter the specified formula adding arbitrary offsets (using the offset function), or creating new terms by using the “I” function. In this brief example, where we will estimate a model that includes networks of size four and five, we will add an interaction effect between the edge-count statistic and the indicator function that equals one if the network is of size 5. This way, while poling the data, we will still be able to obtain different edge-count estimates depending on the number of vertices in the graph.
# Simulating networks of different sizes set.seed(12344) nets <- rbernoulli(c(rep(4, 10), rep(5, 10)), c(rep(.2, 10), rep(.1, 10)))
Fitting an ergmito under the Bernoulli model
ans0 <- ergmito(nets ~ edges) summary(ans0) #> #> ERGMito estimates (MLE) #> This model includes 20 networks. #> #> formula: #> nets ~ edges #> #> Estimate Std. Error z value Pr(>|z|) #> edges -1.68640 0.15396 -10.954 < 2.2e-16 *** #> --- #> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 #> AIC: 279.3753 BIC: 283.1436 (Smaller is better.)
Fitting the model including a reference term for networks of size 5. Notice that the variable -n- and other graph attributes can be used with -model_update-.
ans1 <- ergmito(nets ~ edges, model_update = ~ I(edges * (n == 5))) summary(ans1) #> #> ERGMito estimates (MLE) #> This model includes 20 networks. #> #> formula: #> nets ~ edges + I(edges * (n == 5)) #> #> Estimate Std. Error z value Pr(>|z|) #> edges -1.18958 0.21583 -5.5116 3.556e-08 *** #> I(edges * (n == 5)) -0.90116 0.31250 -2.8837 0.00393 ** #> --- #> Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1 #> AIC: 272.9916 BIC: 280.5282 (Smaller is better.)
The resulting parameter for the edge-count is smaller for networks of size five
We can see that in this case the difference in edge-count matters.
Contributing
Please note that the ‘ergmito’ project is released with a Contributor Code of Conduct. By contributing to this project, you agree to abide by its terms.

